Multilayer matrix factorization with neural network

This project is a proof-of-concept implementation of multilayer NMF, combining ideas from neuralNMF package and Poisson matrix factorization from ASAP package.

Key-idea Given a matrix factorization problem, i.e.

  • $W \sim \theta \beta$ where,
    • $W$ is cell x gene matrix
    • $\theta$ is cell x factor matrix
    • $\beta$ is factor x gene matrix
  • pytorch autograd for the optimization of $\theta$ matrix
  • least squares or PMF method for $\beta$ matrix optimization.
  • neural network for multilayer factorization ( W -> $\theta 1$ -> $\theta 2$) where $\theta$ is new $W$ for each layer.

Reference - Will, Tyler, Runyu Zhang, Eli Sadovnik, Mengdi Gao, Joshua Vendrow, Jamie Haddock, Denali Molitor, and Deanna Needell. “Neural nonnegative matrix factorization for hierarchical multilayer topic modeling.” arXiv preprint arXiv:2303.00058 (2023).

Data prep

We simulate a dataset consisting of 1000 cells with 2000 genes using the Poisson-Gamma model.

############### generate data

import neuralNMF
import scipy
import torch
from neuralNMF.dutil.read_write import write_h5

H,W,X = neuralNMF.generate_data(N=1000,K=10,M=2000,mode='block')
smat = scipy.sparse.csr_matrix(X)
row_names = [ str(i) for i in range(X.shape[0])]
col_names = ['c'+str(i) for i in range(X.shape[1])]
write_h5('data/sim',row_names,col_names,smat)

Run model

In this case, the matrix factorization problem is:

  • $W \sim \theta \beta$ where,
    • $W$ is cell x gene matrix is 1000 x 2000
    • $\theta$ is cell x factor matrix
      • layer 1: $\theta 1$ is 1000 x 20
      • layer 2: $\theta 2$ is 20 x 10
    • $\beta$ is factor x gene matrix
      • layer 1: $\beta 1$ is 2000 x 20
      • layer 2: $\beta 2$ is 2000 x 10 
import neuralNMF
import logging 

sample = 'sim'
wdir = ''
neuralNMF.create_dataset(sample,working_dirpath=wdir)

data_mem_size = 10000
layers = [20,10]
device = 'cpu'
epochs = 300
model = neuralNMF.create_model(sample=sample,data_mem_size=data_mem_size,layers=layers,device=device,working_dirpath=wdir)
logging.info(model.net)

model.train(epochs=epochs,lr=1)
model.save()

Results

import matplotlib.pylab as plt
import seaborn as sns 
import pandas as pd
import anndata as an
import neuralNMF as model

sample = 'sim'
wdir = ''

fpath = wdir+'results/'+sample
adata = an.read_h5ad(wdir+'results/'+sample+'.h5nnmf')

##plot theta
sns.clustermap(adata.uns['theta_l1'])
plt.savefig(fpath+'_theta1.png');plt.close()

sns.clustermap(adata.uns['theta_l2'])
plt.savefig(fpath+'_theta2.png');plt.close()

#plot beta
model.plot_gene_loading(adata = adata,col='beta_l1',top_n=10,max_thresh=50)

model.plot_gene_loading(adata = adata,col='beta_l2',top_n=10,max_thresh=50)
Beta layer 1 (2000 genes x 20 factors)
Beta layer 2 (2000 genes x 10 factors)
Theta layer 1 (1000 cells x 20 factors)
Theta layer 2 ( 20 factors x 10 factors)

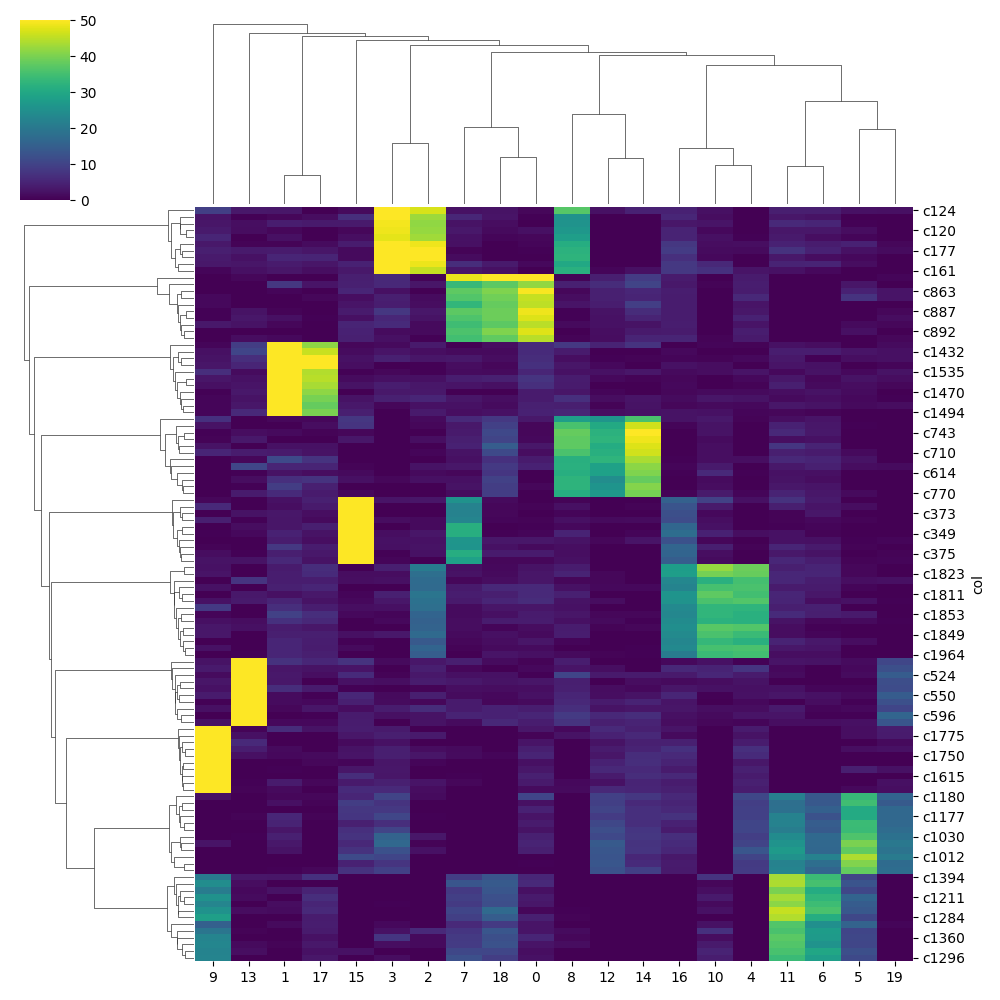
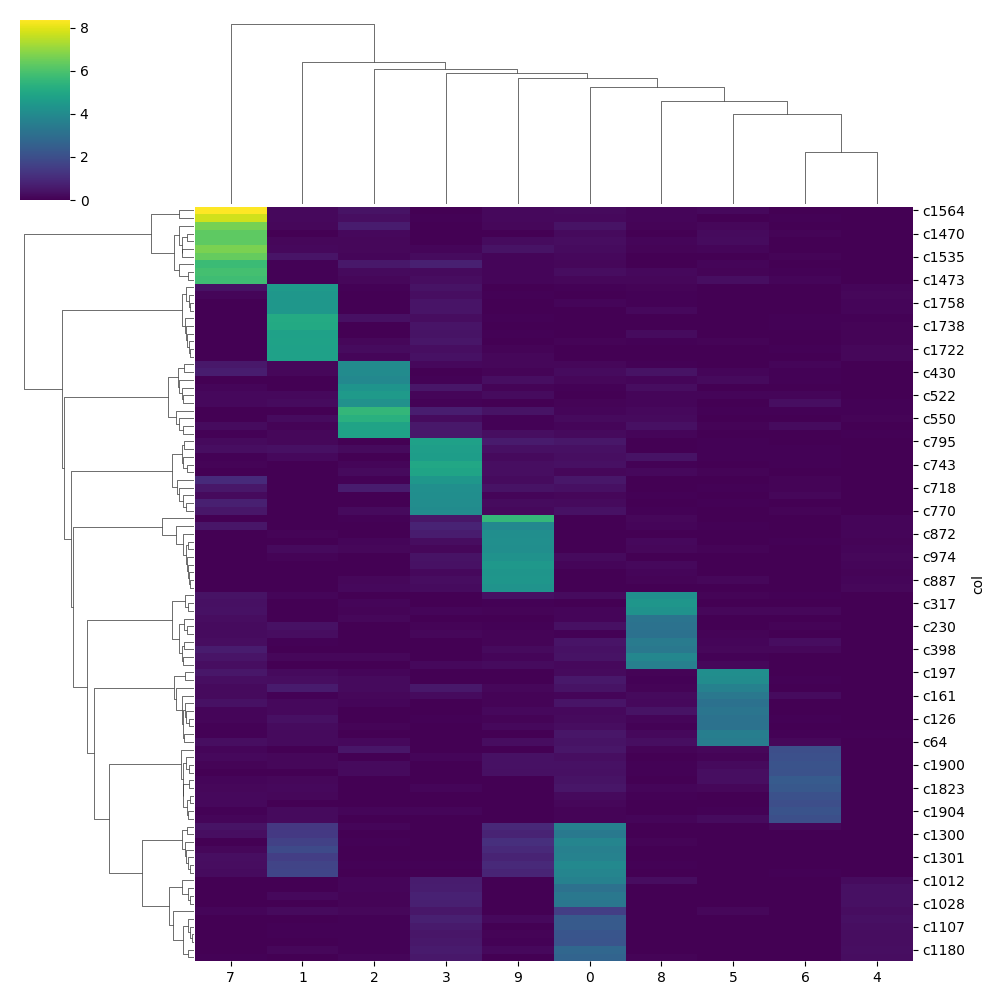
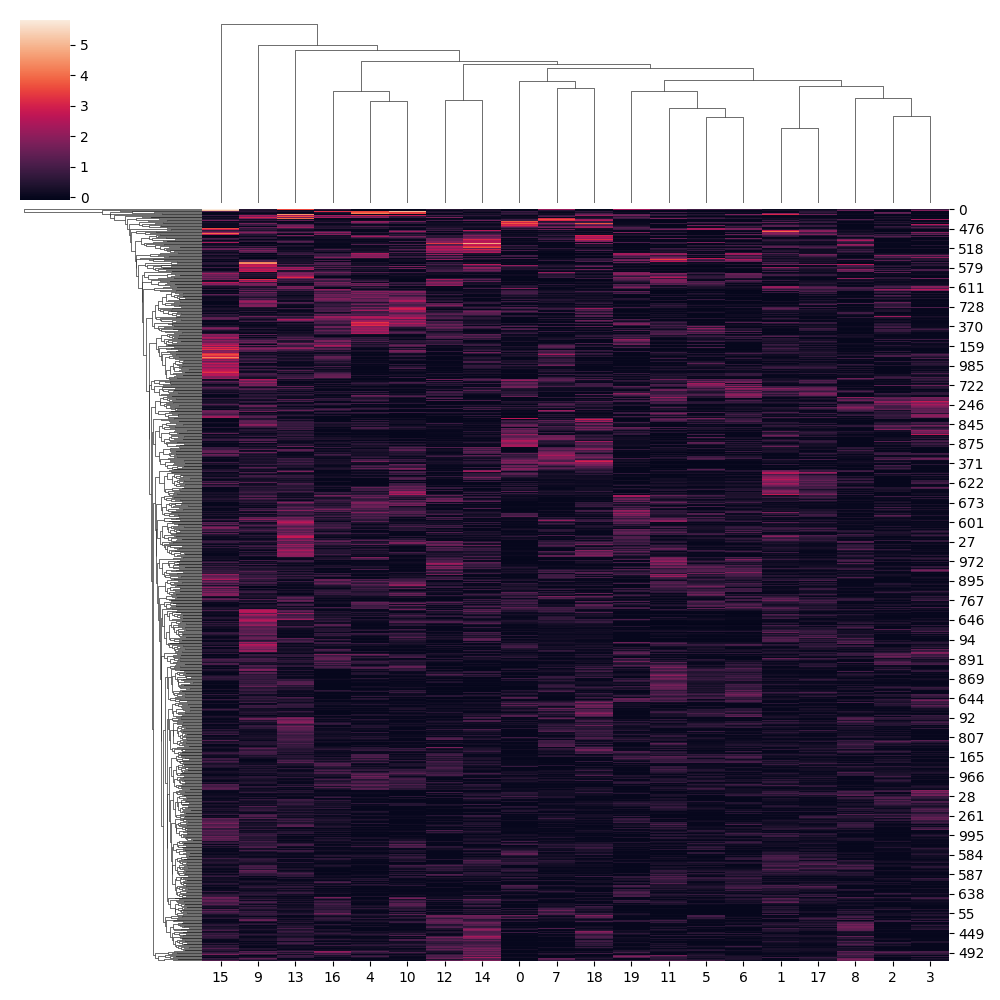
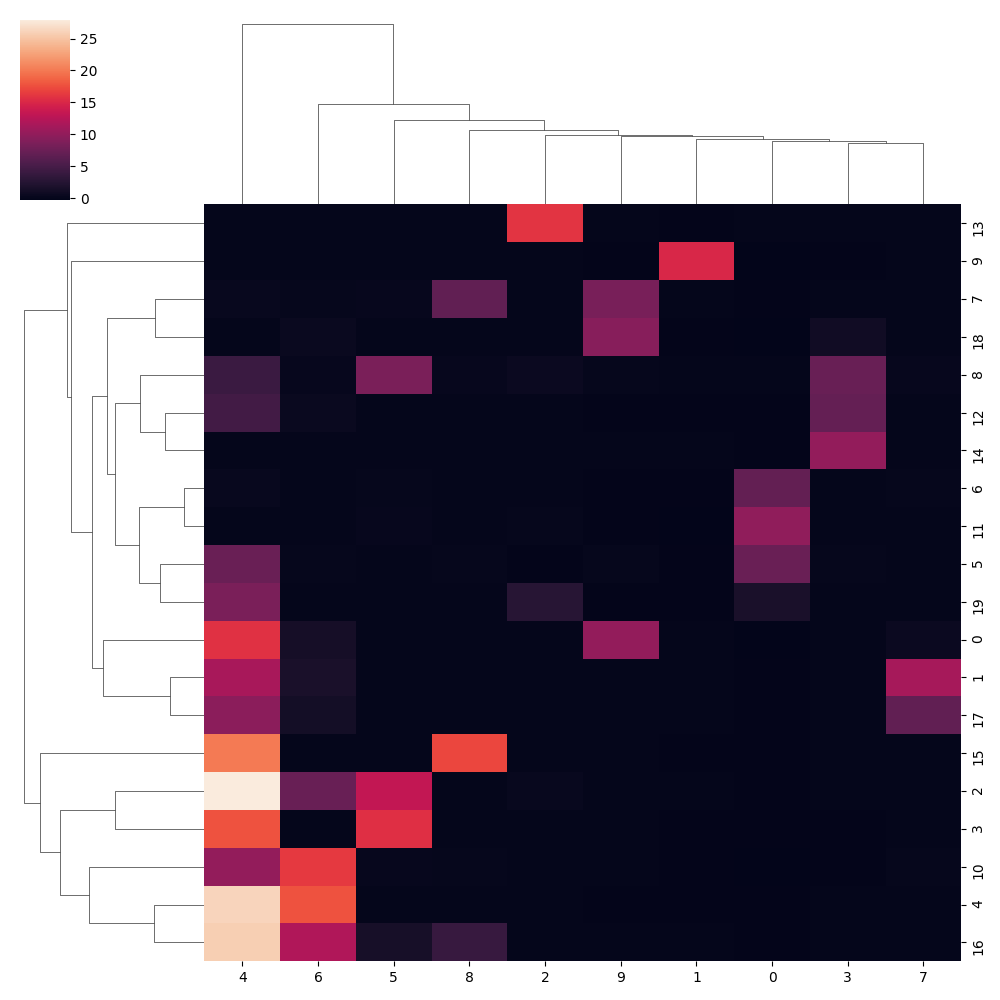
Conclusion

neuralNMF model provides a proof-of-concept modelling framework to integrate neural networks with matrix factorization techniques. To factorize $W \sim \theta \beta$, we optimized $\theta$ as neural network parameters and $\beta$ with factorization reconstruction loss. We can further refine this model to learn both $\theta$ and $\beta$ matrices as network parameters.

The project code used to generate the above results is available neuralNMF.