Data embedding in representation learning

In this project, we discuss computational methods used in the single-cell analysis for embedding gene expression data.

The genomic data is ever-increasing in size and complexity. Technological advancements have enabled us to generate multimodal omics data from millions of cells. This large-scale data poses many challenges for researchers to extract true biological signals for discovery.

One approach to systematically learning complex biological data is to leverage the inherent features of biological mechanisms, i.e., genomic features often act in modules. We are interested in identifying hidden patterns that represent abstract concepts in the data and then linking those concepts to known biological modules or pathways using prior knowledge of genomic features.

How do we learn abstract concepts from biological data?

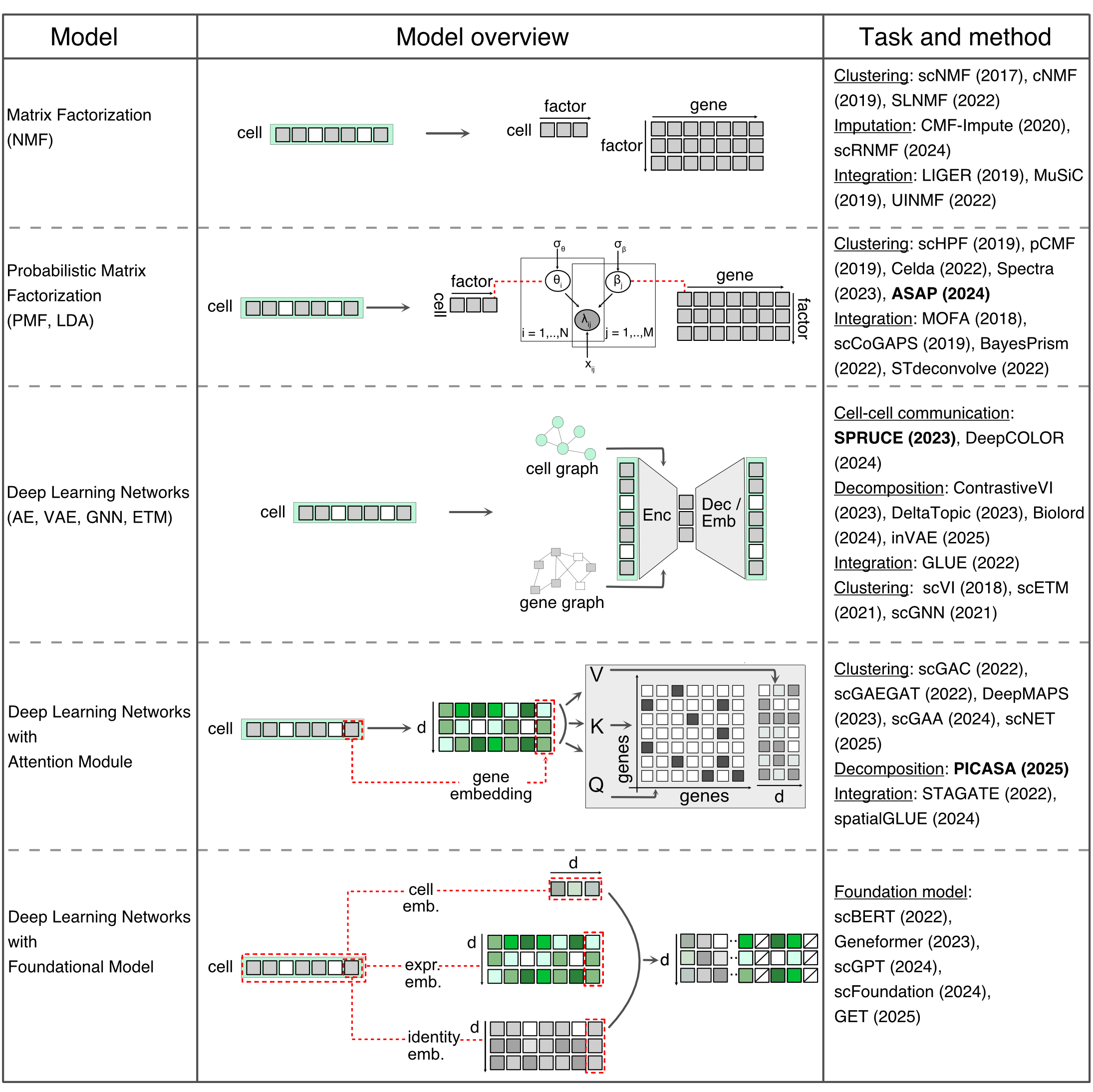
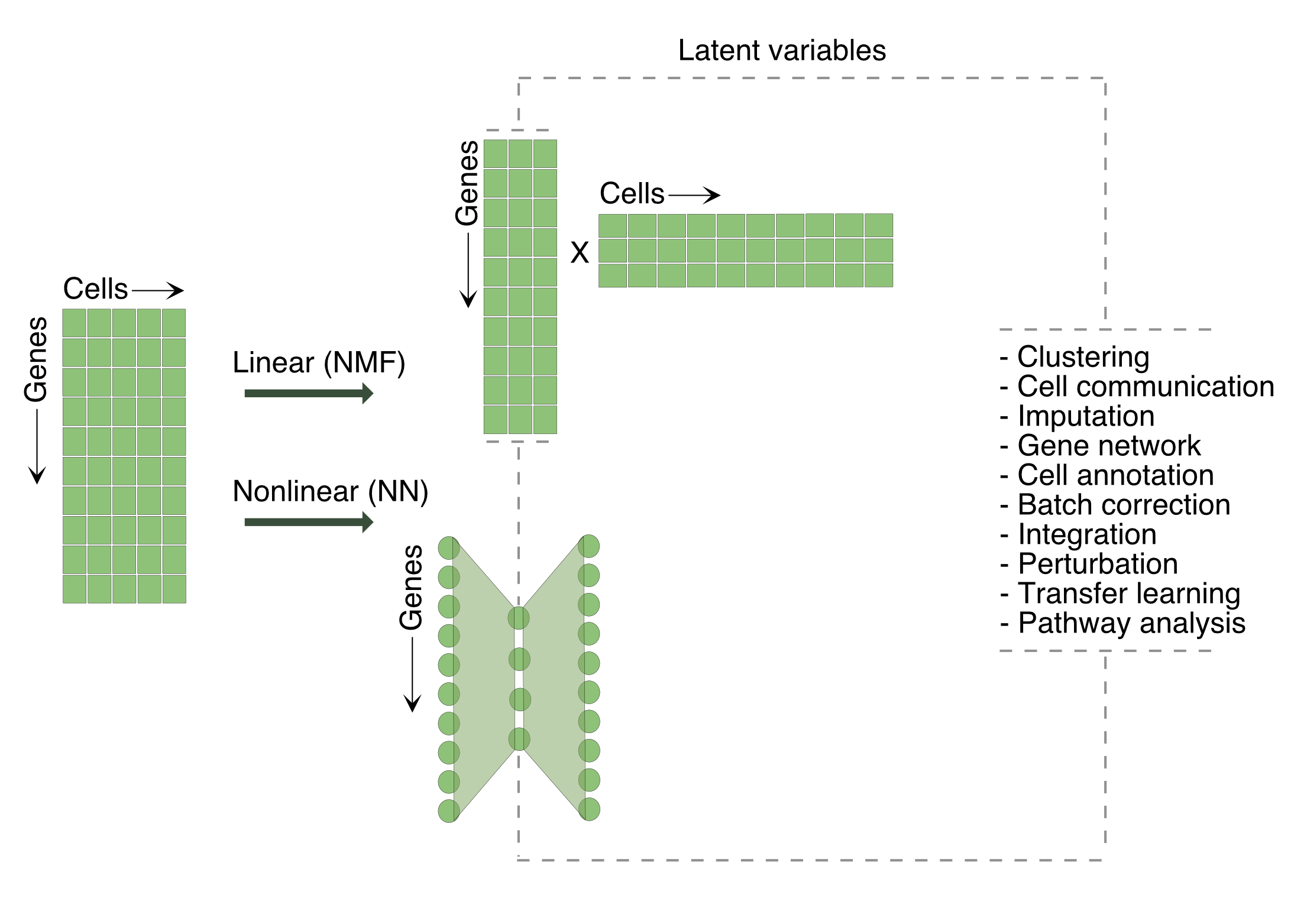
The latent variable model (LVM) provides a framework for learning a set of low-dimensional hidden variables from empirically measured high-dimensional data. The computational methods used for latent variable modelling can be broadly classified into two groups - linear and nonlinear models. The simple linear methods include Principle Component Analysis (PCA). At the same time, complex models consist of probabilistic matrix factorization and Latent Dirichlet Allocation (LDA) models. The nonlinear models are generally based on neural networks, where autoencoders or variational autoencoders (VAEs) represent simpler models. Complex models encompass deep generative networks, including generative adversarial networks (GANs), graph neural networks (GNNs), attention networks, diffusion networks, and large language-based foundation models. Both linear and nonlinear models can be designed within the Bayesian framework to enhance interpretability and incorporate prior knowledge.

A defining feature of LVMs is the assumption that the observed data is generated from latent variables via some underlying generative process. In contrast, when the models are not generative, i.e., do not describe the data generation process, such as contrastive learning, belong to a distinct group of representation learning models. These “model-free” approaches focus on learning latent spaces that reveal hidden structure in the data. Generally, such models are based on neural networks.

Data embedding approaches

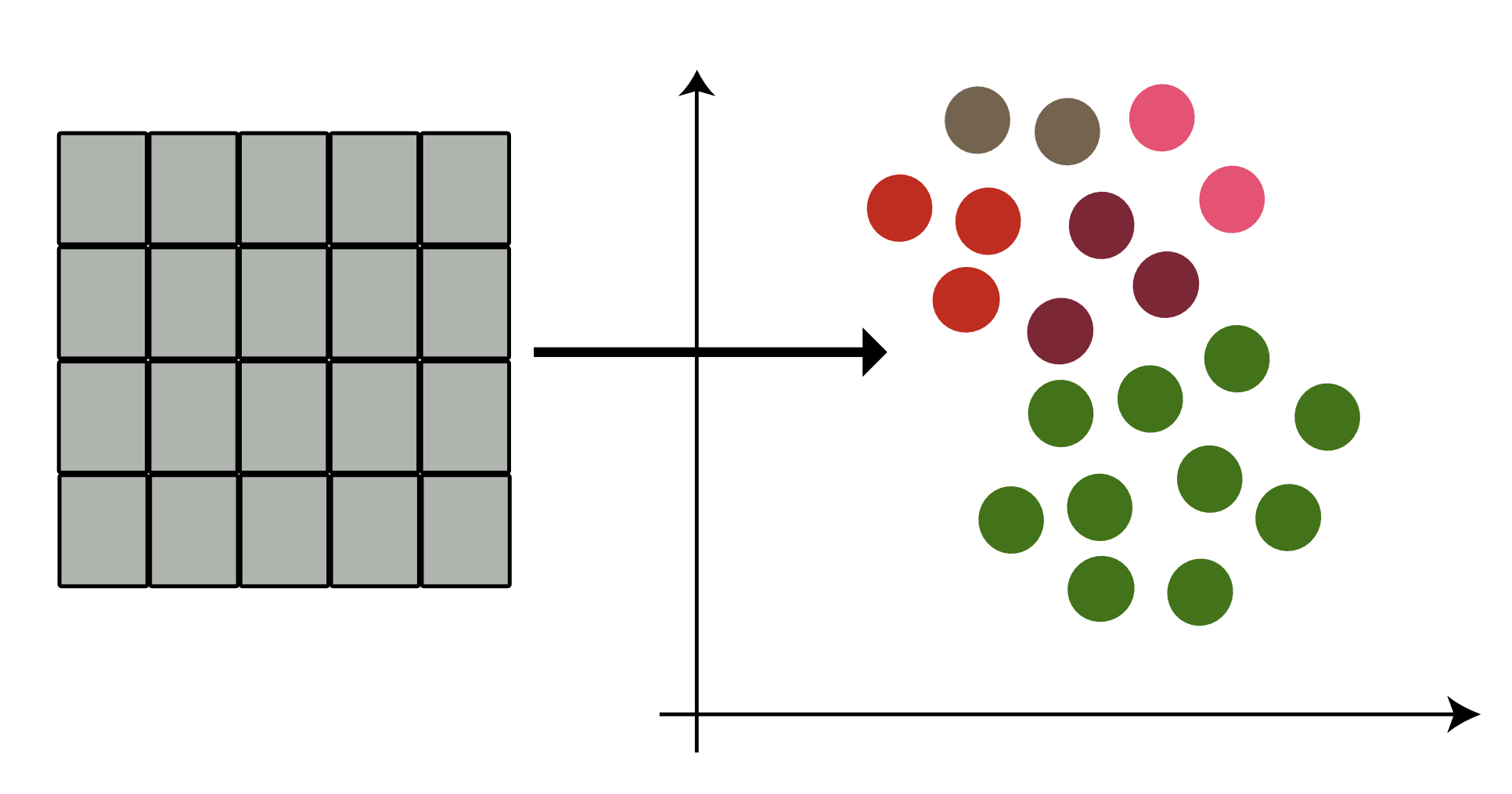
We aim to transform cell embedding in gene space (cell x gene) to factor space (cell x factor), where each factor represents an abstract biological concept.

• Matrix factorization: We approximate the count data matrix by learning two low-dimensional factor matrices that describe the structure of factors across cells and a weight matrix that specifies the contribution of each gene to inferred factors. This is a single transformation from gene space to factor space.

• Probabilistic Matrix Factorization: Adding parametric layers is desirable for modeling gene count data, as it handles non-negative sparse datasets with high noise levels and missing values. This provides a multi-layer transformation from gene space to factor space.

• Neural networks: Linear approximation of latent factors may not fully capture the complex structure of biological data. A neural network applies multiple nonlinear transformations and learns an abstract feature representation that captures the most informative structure. Additionally, graph layers incorporate topological information of cells into the model, while embedding layers provide better interpretability of latent spaces.

• Attention networks: In the above methods, we directly embedded cells in latent space. Instead, we add a step of embedding for each gene using attention networks, such that relationships among genes are incorporated into the latent space.

• Foundation networks: Neural networks with attention layers, as above, do not generalize across datasets. To learn a robust and generalizable network, we make two important changes: First, we assign an identity to each gene and learn identity-specific embeddings in addition to expression embedding. Second, we also assign an identity to each cell, such as cell type and disease state, and include its embedding in the training. These models are “foundational” in nature and learned parameters can be applied across different biological experiments.

The following table provides a summary of different data embedding techniques used in single-cell data analysis.